Application Note SoftMax Pro ソフトウェアで
ベストcurve fitをセレクト
- 21種類のcurve fitオプションの中から最適な方法でデータをグラフ化
- Parameterの独立性機能を用いて、特定のcurve fitの適合性を評価
- 推定相対効力および平行線解析のためにglobal curve fitを適用
- 同一グラフ内のplotに対して独立したcurve fitを適用
PDF版(英語)
はじめに
変化率、curveの上下漸近線、EC50/IC50値など、データの重要な特性を決定する際、正しいcurve fitモデルをセレクトすることは極めて重要です。したがって、curve fitの目標は、データに最も近いparameter値、言い換えれば経験的データを表す最適な数式を見つけることです。SoftMax® Pro ソフトウェアには、 four parameter logistic(4P)および five parameter logistic(5P)非線形回帰モデルを含む、21種類のcurve fit optionが用意されています。これらは、選択されたモデルのカーブフィットcurve fit parameterを調節してデータに最適にフィットさせることにより、plotされたcurveが濃度対反応の関係を表現するcurveにできるだけ近くなるようにします。
このテクニカルノートでは、SoftMax Proで利用可能なさまざまなリニアおよびノンリニア回帰モデルについて解説しています。さらに、二乗誤差の合計(SSE)および赤池情報量規準(AIC)を用いたプロトコールを実装し、データを最も適切に表現するcurve fitモデルの評価を行っています。
リニア回帰
データを分析する最も簡単な方法は、リニア回帰curve fitである。これは方程式 \( y = A + Bx \)で表され、x(一般に濃度)は独立変数、y(応答)は従属変数です。直線の傾きはBで、Aはx=0のときのy切片です。SoftMax Proには3つのリニア回帰curve fitがあります。リニア(\( y = A + Bx \))、半対数(\( y = A + B \cdot \log_{10}(x) \))、対数対数(\( \log_{10}(y) = A + B \cdot \log_{10}(x) \))です。SoftMax Proはデータを通る最良の直線を求めます(図1)。アッセイの直線範囲は、x軸上に最低3つのデータポイントを使用して決定できますが、適合の精度を向上させるために、指定された範囲内の標準濃度を追加する必要があります *1。この方法の第一の利点はシンプルなことです。しかし、ほとんどの場合、測定値と測定変数の関係はノンリニアです。
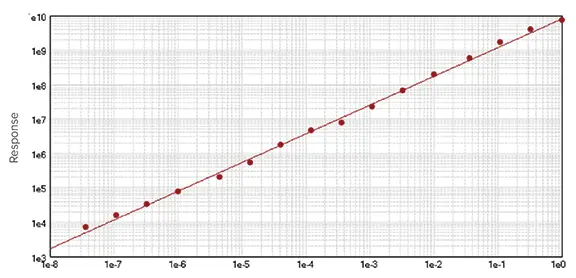
図1. linear curve fitの例。
ノンリニア回帰
ノンリニアデータは,一般にロジスティック回帰を用いてモデルされます。この場合,測定値と測定変数の間の関係はノンリニアです。目的はまた,測定値と期待値の間の偏差を最小にするそれらのパラメータ値を見つけることです。正しいfitを選択するためには、モデルcurveの一般的な形状を理解し、data pointの形状と比較することが重要です *2。
SoftMax Pro では、17種類のノンリニア回帰curve-fittingが利用可能です。これらには以下のモデルが含まれます:
・二次関数(Quadratic)
・三次関数(Cubic)
・四次関数(Quartic)
・対数ロジット(Log-Logit)
・三次スプライン(Cubic Spline)
・指数関数(Exponential)
・長方形双曲線(Rectangular Hyperbola、線形項あり/なし)
・2パラメータ指数関数(Two-Parameter Exponential)
・二重指数関数(Bi-Exponential)
・二重長方形双曲線(Bi-Rectangular Hyperbola)
・二部位競合モデル(Two Site Competition)
・ガウス関数(Gaussian)
・Brain-Cousens モデル
・4パラメータロジスティック(4P)
・5パラメータロジスティック(5P) 5Pオルタネート(5P Alternate)
SoftMax Proは、可能な限り最良のcurve fitを実現するために、ノンリニアcurve fit処理で最も広く使用されている反復手順、Levenberg-Marquardtアルゴリズムを実装しています。
最も一般的な2つのノンリニアcurve fitは4Pと5Pで、S字カーブを描くシグモイド関数です(図2)。4Pと5Pのcurve fitには、それぞれ少なくとも4つのデータ点と5つのデータ点が必要ですが、これらの回帰タイプでは少なくとも6つのデータ点を使うことで、より正確なfitが得られます *1。4P curve fitは、次の式で記述されます:
$$ y = \left( \frac{A - D}{1 + \left( \frac{x}{C} \right)^B} \right) + D $$
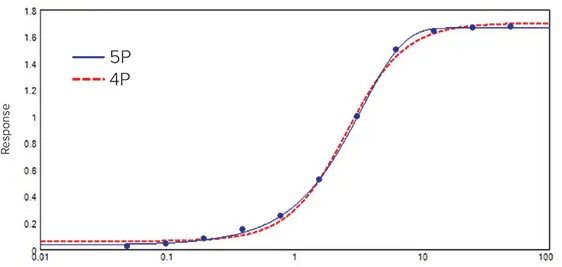
図2. 比較のために4Pと5Pのcurve fitモデルでfitした濃度反応curve。4Pモデルは滑らかな対称curveを与えますが、データは明らかに非対称です。したがって、5Pモデルの方がより適合度が高いです。
ここで、yは反応、Dは分析物濃度無限大での反応、Aは分析物濃度ゼロでの反応、xは分析物濃度、Cは変曲点(EC50/IC50)、Bは傾き係数です。ADの場合、反応は濃度とともに増加します。4P curve fitは対称関数であり、curveの半分はEC50/IC50を中心にもう半分と正確に対称です。
しかし、免疫学やバイオアッセイのデータの中には対称でないものもあり、さらに柔軟性が必要なものもあります。そのような状況では、5Pモデルの方がうまくいくかもしれません。5Pモデルは、もう1つのパラメータG(図2)を追加することで、非対称なdata fittingを可能にするからです。一般的な式は以下の通りです:
$$ y = \left( \frac{A - D}{\left(1 + \left( \frac{x}{C} \right)^B \right)^G} \right) + D $$
非対称パラメータは、curveの各半分が異なることを許容します。しかし、非対称性が小さい場合、特に平行線分析(PLA)をアッセイに使用する場合は、4P curve fitを使用することをお勧めします。
ベストなcurve fitセレクトについて
正確で精密なデータを得るためには、curve fit、特にstandard curveの全体的な良し悪しを評価する必要があります。curve fitモデルを評価する際には、複数の実験を行うことが重要です。R2値は一般にfitの良し悪しをよく表しています。R2値が0.99以上であれば、非常に良好なfitとみなされます。しかし、R2値は、特に標準偏差がサンプル濃度によって変化する場合、誤解を招く可能性があります *3。理想的には、標準偏差はすべての試料濃度で同じであるべきですが(同相統計データ)、必ずしもそうではなく、標準偏差は一般的に試料濃度とともに大きくなります(異相統計データ)。データを正規化するために開発された方法には、F統計量を用いた二乗誤差の和(SSE)法と赤池情報量規準(AIC)法があります。どちらの手法も、得られた値と予測値(セレクトしたcurve fitによる)の誤差を評価するもので、非常によく似ています。
SSE法は、残差と残差プロット(残差対濃度)を用いるので、残差平方和法とも呼ばれます。残差は、各濃度における反応 y と選択したcurve fitから得られる予測反応 ŷの差です *4:
$$ \text{Residual} = \text{data} - \text{fit} = y - \hat{y} $$
残差はランダム誤差を表します。したがって、セレクトしたcurve fitがデータに対して正しい場合、残差は残差plotのゼロ線の周りにランダムに散らばって見えるはずです(図3A)。残差プロット(図3B)で残差が系統的なパターンを示すなら、それはモデルがデータにうまくfitしていないことの明らかなサインです。
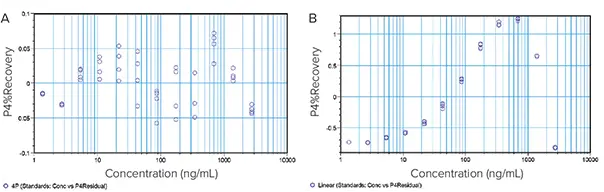
図3. リニアcurveモデルと4P curveモデルにfitさせたデータの残差plot。(A)Plotされた残差はゼロを中心にランダムに散らばっており、4Pモデルがデータをよく説明していることを示しています。(B) 残差は系統的なパターンを示し、線形モデルがデータにうまく適合していないことを示しています。
SSEは以下の式で求められます:
$$ \text{SSE} = \sum_{i=1}^{n} w_i (y_i - \hat{y}_i)^2 $$
SSEを最小化することで、データ誤差が独立で正規分布しているという仮定に基づくモデル・パラメータの最尤推定値が得られます。ベストのcurve fitは、パラメータが最小のSSEを生成するものです。もし両方のモデルがデータに分別なくfitするなら、最小のSSEを与えるplotが使用すべき最良のものです。
2つのモデルが入れ子になっていて、一方が他方の特別な場合、例えば4PがG=1の5Pの特別な場合、より詳細な式(より多くのパラメータ)を持つモデルは、もう一方のモデルより小さいか等しいSSEを持つことが保証されます。これは、より多くのパラメータを持つモデルは、より多くの変曲点をデータに適合させることができるからです *4。したがって、どのモデルがデータに最もフィットするかを決定するために、F検定とF確率という追加の統計計算が必要となります。F確率は、F検定とcurve fitモデルに関連する自由度を用いて、SSEの減少が偶然に起こったかどうかを評価します。通常、0.05(信頼度95 %に相当)以下の確率がしきい値として使用され、最も詳細な式を持つモデルがデータをよりよく表現していることを意味します。
AIC法は、尤度統計量を用いて、一方が他方の特別な場合である2つのcurve fitモデルについて、与えられたデータの適合度を比較します。AICは、正規分布誤差を持つデータのSSEを用いて、次のように計算できます:
$$ \text{AIC} = n \cdot \log\left(\frac{\text{SSE}}{n}\right) + 2K $$
ここで n は標本サイズで、K は曲線を記述するパラメータの数です。標本サイズが小さい場合(すなわち、\( \frac{n}{K} \lesssim 40 \))、代わりに2次の赤池情報量規準(AICc)を使用すべきです。
$$ \text{AICc} = \text{AIC} + \frac{2K(K+1)}{n - K - 1} $$
ここで n は標本サイズで,K は曲線を記述するパラメータの数です。標本サイズが大きくなるにつれて,AICcの最後の項はゼロに近づき,AICcはAIC5と同じ結論をもたらす傾向があります。AICとAICcは、統計的な適合の良さと、この特定の適合度を達成するために推定しなければならないparameterの数の両方を考慮に入れています。AICは、parameterの追加にペナルティを課すので、適合は良いがparameter数が最小のモデルを選択します。AICまたはAICcの値が低いカーブフィット処理は、好ましいモデル、すなわち、データによくフィットする最小のparameterを持つモデルを示します *5。
どちらの方法も、どのcurve fitがデータを最もよく記述するかを決定するのに有用ですが、帰無仮説を検定するという意味でのモデルの検定は提供しません:すなわち、fitの良し悪しに関する情報は提供しません。つまり、適合の良し悪しに関する情報は得られないのです。もし悪いモデルだけを考慮すれば、論理的には悪いモデルの中から最良のものを選ぶことになります。curve fitは、与えられたモデルのベストなparameterを見つけたり、2つのモデルを比較したりすることができますが、候補となるモデルは、過去の調査や科学的な考察に基づくべきです。データを説明するのに妥当なモデルの集合を特定した後、解析を行う前に、その集合の中で最も複雑なモデルとして定義されるグローバルモデルの適合性を評価すべきです。一般に、グローバルモデルが適合すれば、より単純なモデルも適合すると仮定できます。
適合度の測定
SoftMax Pro 7には、データセットに対する所定のcurve fitの適合性を調べるための1つの方法「Independence」という新しいparameterが実装されています。parameterの依存性は、あるparameterの最適値が他のparameterの最適値にどの程度依存するかを示す尺度です。2つ以上のparameterからなるcurve fitモデルの場合、curveを記述するparameterは絡み合っているか(Independenceが1である理想的なケース)、または冗長である(Independenceが0である最悪のケース)のいずれかです。
セレクトしたcurve fitでデータをfittingした後、1つのparameterを変更すると、曲線はデータ点から遠ざかります。固定されたparameterを補正するために他のparameterの値を変更し、曲線が点に近づいたが、最初に設定したものとは異なるcurve fitになった場合、parameterは絡み合っていることになります。一方、curveが元の位置に戻る場合は、parameterは冗長です。
Independenceは0と1の間の数値で、1が理想的です。グラフ凡例にIndependenceを表示するには、curve fit処理のアイコンをクリックします(図4)。curve fit settingウィンドウが現れます。Statisticsタブを選び、「Calculate Parameter Dependencies」にチェックを入れるだけでよい。
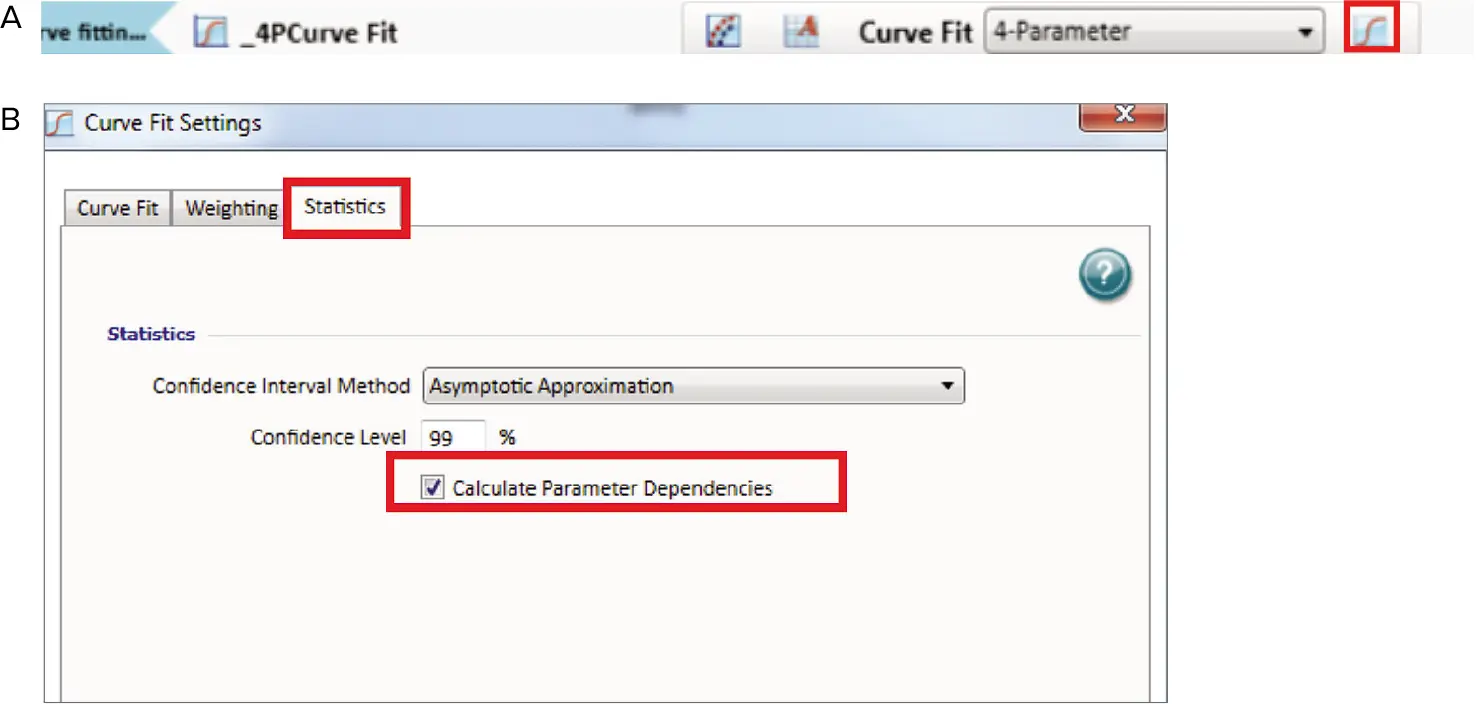
図4. (A) Menu (B) Curve fit settings
グラフの凡例に、曲線を記述する各parameterのIndependenceが表示されるようになりました(図5)。
図5のgraph fitの凡例では、パラメータのIndependenceが対数スケーリングのバーに変換されています。棒グラフが10本の場合は、独立性が高いことを示します。非常に小さな値だけが問題を示しますので、この変換にはノンリニア変換が使われています。1つまたは複数のparameterに棒グラフがほとんどないか、まったくない場合は、curve fitがdata setに合っていない可能性があります。
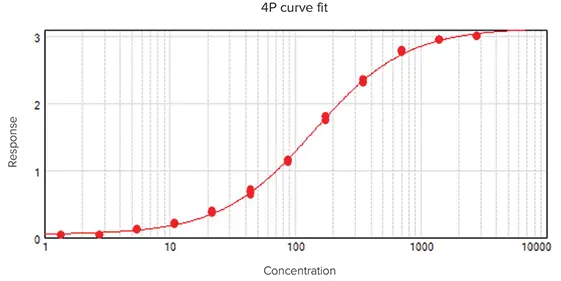

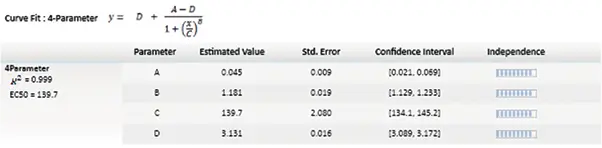
図5. parameter independenceを示すグラフの凡例。独立性は棒グラフに変換され、10本の棒グラフはindependenceが高いことを示しています。
例えば、 data setがシグモイド状で、下側と上側の漸近線がはっきりしている場合、4P fitが適切で、すべてのparameterについて多くの棒グラフがある。しかし、片方または両方の漸近線が欠落している場合、AまたはD parameterは棒グラフが少なく、data setから信頼できる値が推測できないことを示します。
利用可能なプロトコール:Curve Fitting Evaluation
SoftMax Proでは、データ入力時にSSE、F確率、AICc値を自動的に計算するプロトコール「Curve Fitting Evaluation」が開発されています。SSE法とAICc法を用いたcurve fit処理の結論と、関連するすべての計算を封じ込めた結果セクションが実装されています(図7)。プロトコールはSoftMax Proプロトコールホームからダウンロードできます。
以下の例では、4P(図6A)と5P(図6B)のcurve fitモデルにデータをfit処理しました。
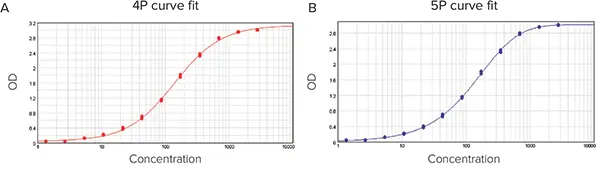
図6. curveモデルにfit処理したデータ。(A) 4P curve fit。(B) 5P curve fit。

図7. SSEとAICcテスト。curve fit評価プロトコールを用いて4Pおよび5P curveモデルにfittingしたデータ結果。
SSE法は、4Pと5P curve fit モデルのSSEがそれぞれ0.058と0.027で、5P curve fitモデルが4Pよりも良い選択であることを示しました。問題は、4P curve fit モデルが5P curve fitモデルの特殊なケースであったことです(4PはG=1の5Pである)。したがって、5P curve fitモデルは、少なくとも4Pと同程度には優れていました。追加の統計量が必要でした。F検定(61.539)とF確率(0.000)は、この例では5P curve fitモデルが4P curve fit モデルよりもデータをよく表現していることを確認しました。AICc法もまた、5Pが4P curve fitモデルよりもデータによくfitすることを示しました: AICcは、4Pが-405.365、5Pが-447.945でした。最後に残差plotでは、残差がゼロラインの周りにランダムに散らばっており、どちらのcurve fitモデルもデータに対して正しいことが確認されました(図8)。これらのテスト方法を総合すると、5P curve fitモデルの方がデータへの適合性が高いことが示されました。
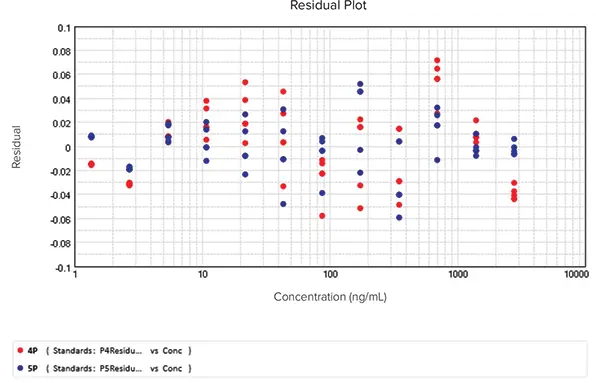
図8. 4Pおよび5P curveモデルにfitしたデータの残差plot。
サマリー
SoftMax Pro 7には、広く使用されている4Pおよび5P curve fit モデルを含む、幅広い数学モデルが用意されています。R値は、データのcurve fitの質を測る尺度としては不十分な場合があります。F確率を用いたSSEとAICc法は、fitの良し悪しを比較し、確信をもって最善のcurve fitモデルをセレクトするのに便利です。しかし、最初のステップは、どちらのモデルもデータが感覚的な値でfitし、科学的な意味を持つことを確認することです。SoftMax Pro 7には、curve fitの良し悪しを推定するためのparameter dependencyの計算方法が搭載されています。得られたparameter independenceはグラフの凡例に視覚的に表示され、データの解釈を容易にします。
参考文献
- Davis D, Zhang A, Etienne C, Huang I, and Malit M. Principles of curve fitting for multiplex sandwich immunoassays. Rev B Tech Note 2861. In. Bio-Rad Laboratories, Inc, Hercules, CA. 2002.
- Ledvij M. Curve fitting made easy. The Industrial Physicist. 2003; 9:24-27
- Kiser MM and Dolan JW. Selecting the best curve fit. LC-GC Europe. March 2004; 138-143
- Gottschalk PG and Dunn JR. The 5-Parameter Logistic: A characterisation and comparison with the 4-Parameter logistic. Analytical Biochemistry. 2005: 343:54-65.
- Burnham KP and Anderson DR. Model Selection and Multimodel Inference: a practical information-theoretic approach. 2nd edition. New York: Springer-Verlag, 2002.
- Cooch EG and White GC. Program MARK: Analysis of data from marked individuals, a ‘gentle introduction’. www.phidot.org/software/mark/docs/book. 2001.
SoftMax Pro 7 ソフトウェアの詳細はこちら >>
PDF版(英語)